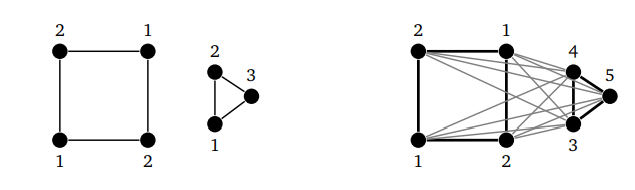
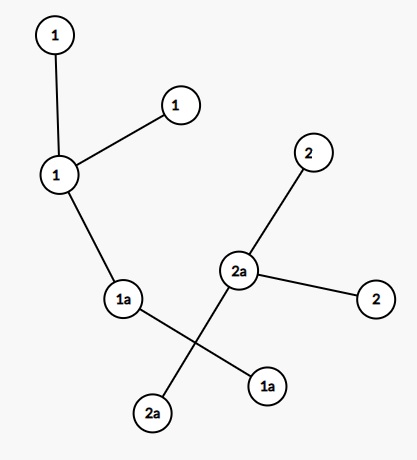
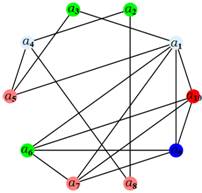
Минимальная раскраска графа

Раскраски и укладки графов
Визуализация графа, поиск кратчайшего пути и многое другое. В разделе Справка вы найдете обучающие видео. Для мультиграфа матрица содержит значения минимальных дуг между вершинами. Мартрица имеет неправильный формат.




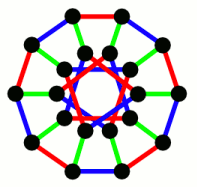
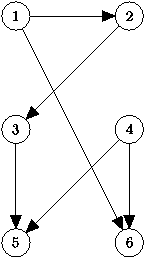


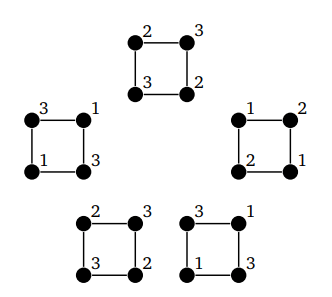


Раскраска графа — теоретико-графовая конструкция, частный случай разметки графа. При раскраске элементам графа ставятся в соответствие метки с учётом определённых ограничений; эти метки традиционно называются «цветами». В простейшем случае такой способ окраски вершин графа , при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин.


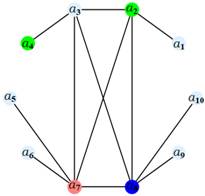



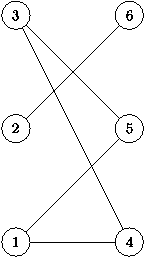




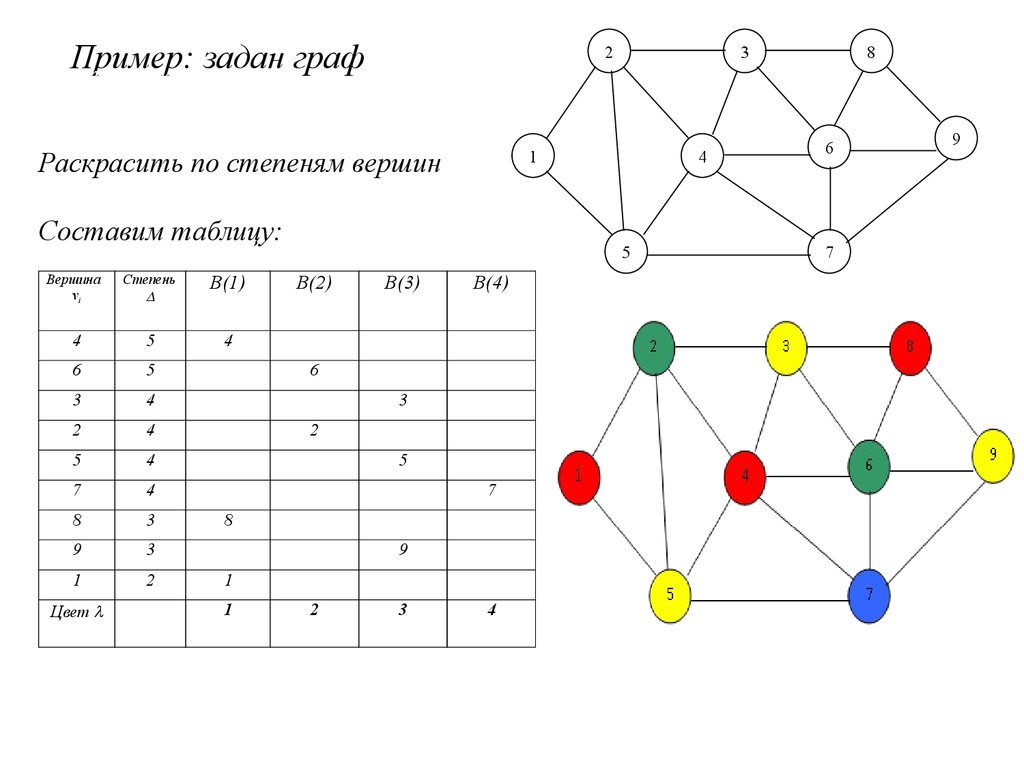
В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах. Также покажем примеры раскраски графов разных типов, так как в каждом случае этот процесс немного отличается. Цвета — это целые положительные цифры.